1. 概念

　　首先我们得知道进制的概念。所谓的进制，也叫做进位计数制，这是人为定义的带进位的计数方法。当然也有不带进位的计数方法，比如原始的结绳计数法，唱票时常用的“正”字计数法等。

　　任何一种进制，每一位上的数在运算时都是满X进一位。比如十进制是逢十进一，十六进制是逢十六进一，二进制就是逢二进一，以此类推，X进制就是逢X进1位。以我们最熟悉的十进制为例，每逢十进一，当数为19时，下一位数的尾数便满足该进制的最大数，于是下一位末位清零，前置位+1，变成20。

　　2. 分类

　　在计算机中，目前常用的进制有如下几种：

　　●十进制；

　　●二进制；

　　●八进制；

　　●十六进制

　　因为在计算机的底层只能处理二进制格式的数据，也就是0和1，其他的文字、数字、字符等信息都要转换成二进制的格式，计算机的底层才能识别处理。所以作为一个程序员，二进制是我们必须要理解和掌握的哦。

　　3. 二进制

　　作为一个程序员，必须要掌握的进制就是二进制了，其实我们只需要参考十进制就可以很容易理解进制的问题了。所谓的二进制，里面只有0和1，且满二进一，所以在二进制里是看不到>=2的数的。比如二进制的前10位数分别是0、1、10、11、100、101、110、111、1000、1001。

　　4. 八进制

　　八进制中有07共8个数字，但没有8哦，其规则是满八进一，所以7的下一位数不是8，而是10。17的下一位数不是18，而是20。比如八进制的前10位数分别是0、1、2、3、4、5、6、7、10、11......

　　5. 十六进制

　　十六进制中有0F共16个数字，同样没有16，其规则是满十六进一。在十六进制中，这16个数字分别是0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。即9的下一位不是10，而是A，10这个数只是十进制的衍生物，这一点大家要注意！

　　同理，在十六进制中，19的下一位不是20，而是1A，1F的下一位才是20；99的下一位是9A，FF的下一位才是100。

　　6. 原码、反码与补码

　　6.1 原码

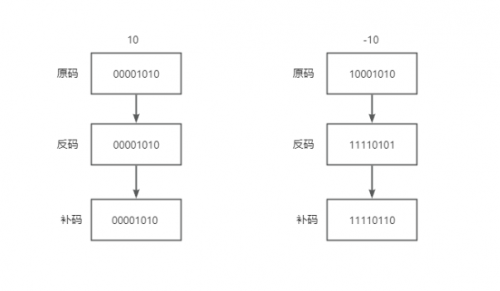
　　对一个正整数来说，所谓的原码，就是指一个整数对应的二进制，比如整数10的原码就是00001010。所以原码就是一个正整数原本对应的二进制形式。但负数的原码和正数却不一样，负数的原码要将正数原码的符号位(最高位)改为1，比如-10的原码就是10001010。

　　6.2 反码

　　正数的反码就是其原码，即正数的原码和反码完全相同。而负数的反码则是将原码中除符号位以外的所有位(数值位)都取反，即 0 变成 1，1 变成 0。如10的原码和反码都是00001010，而-10的原码是10001010，反码则是11110101。

　　6.3 补码

　　正数的补码就是其原码，所以正数的原码、反码、补码都相同。而负数的补码是其反码加1，-10的原码是10001010，反码则是11110101，补码则是11110110。我们可以认为，补码是在反码的基础上打了一个补丁，进行了一点修正，所以叫做“补码”。

　　所以原码、反码、补码的概念只对负数有实际意义，对于正数来说，原码、反码、补码其实都是一样的，如下图所示：

　　7.作用

　　在Java中，进制转换可以用来在不同的进制之间转换数字。以下是一些进制转换的应用：

　　1.二进制和十六进制是计算机中常用的数字表示方法。转换为这些进制可以方便地表示和处理二进制和十六进制数据。

　　2.进制转换也是密码学中的重要概念。例如，在加密和解密过程中，需要将数字转换为不同的进制，以实现安全传输和存储。

　　3.在算法和数据结构中，进制转换也很常见。例如，将一个数字转换为二进制可以方便地实现位运算，这在许多算法中都有用。

　　4.进制转换还可以用于显示数字。例如，在编写计算机程序时，需要将数字转换为字符串，并以不同的进制进行显示。

　　5.进制转换是计算机科学的基础知识之一，对于理解计算机的工作原理也是很有帮助的。

上一篇

java全局变量

下一篇

xml解析器